



We have determined quite a bit about rotational motion. We have also hinted
about the connection between translational motion and rotational motion. For
example, we started from the definition of radian measure that a point mass
traveling a circular path of radius r travels an arc-length s by undergoing an
angular displacement, theta and that, by the definition of radian measure, s =
r*theta.

Through this relationship we determined that the transverse speed of the point mass would be v = r*omega where v = ds/dt and omega = d(theta)/dt. We then generalized things more by showing that we could consider the rotation of solid objects by using the same mathematical description. So, for example, if a thin string is wrapped around the diameter of a cylinder or wheel or sphere of radius r, then a rotation of the cylinder through an angle theta leads to an amount of string of length s = r*theta unwound (see the Maple file for a demonstration) where theta is the angular displacement of the cylinder/wheel/sphere from its original orientation. This only works if the string unwinds from the diameter without slipping.
This mathematical description was useful in finding the motion of a classic
problem: the half-Atwood machine where the pulley wheel of radius R, instead of
being massless, now has a mass, m3, and therefore a rotational
inertia.

The translational motion of the two blocks, m1 and m2, is connected to the rotational motion of the pulley if we assume that the string does not slip on the pulley. The definition of non-slipping is that, if the blocks move by a distance y, then the pulley turns by an angle theta such that y = R*theta. Furthermore, our experience with see-saws and the work-energy theorem applied to rotational motion led us to conclude that the analogous description of "acted upon" for changing rotational motion was the torque, r*Fperp where r is the distance from the action of the force to the axis of rotation and Fperp is the component of force which acts in a direction perpendicular to a vector along r.
The next logical step for generalizing our description still further is to
consider motion which is rolling motion. We
tend to naturally think of this as a combination of translational motion and
rotational motion. Consider a round object of radius R which can undergo
translation, rotation, or a combination of the two as shown here. The rotation
occurs about an axis that is perpendicular to the page and goes through the
geometric center of the object.
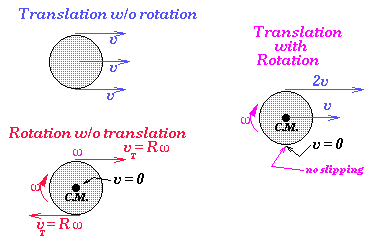
We have pointed out three points on our object, one at the top, one at the geometric center (which we assume is also the location of the center-of-mass since we assume the object is uniform), and one at the bottom. The velocity, relative to a stationary observer, is also shown for each of these points for each of the three cases: translation, rotation, translation and rotation. We get these velocities by first noting that the object is rigid and therefore each point must have the same angular velocity with respect to a rotation axis through the geometric center (the definition of a rigid object). The determination of the actual velocity is given by using what we know about velocity as a vector: we can add velocity vectors to get the net velocity relative to an observer in a non-relativistic reference frame. Hence, in the translation case the velocity of each point must be the same as the velocity of the center-of-mass for a rigid object. For the rotation case, the transverse velocity of each point is given by summing its translation velocity (which is zero) and the transverse velocity from rotational motion, vT = R*omega. In the case of translation and rotation, the net velocity of the three points is again obtained by adding the non-zero translational velocity and the non-zero transverse velocity. If we adjust omega so that R*omega = vT = v, the same v as the translational velocity of the center-of-mass, then we define the object with translational and rotational motion to be rolling without slipping.
Under the rolling without slipping condition, the arc-length of a path along the surface of the object as it rotates matches the translational distance traveled by the center of the object (see the Maple file for an illustration). The crucial point to notice is that in order to have rolling without slipping of a round object on a level surface, we must have the point in contact with the level surface be instantaneously at rest! This is counter-intuitive since the "point in contact" of the round object and the surface it rolls on are constantly changing with time. However, the instantaneous velocity of whichever point is "in contact" is always zero for the instant that contact is made. This has real meaning in considering how rolling motion happens. For example, if there is friction between the surface of the rolling object and the surface it rolls on, then rolling without slipping corresponds to static friction acting. This is not counter-intuitive. If you've driven a car under icy or very wet conditions, you've probably experienced, at least momentarily, a condition in which the wheels are rolling AND sliding. The normal condition for driving is that the wheel moves on the road surface so that rolling without slipping is maintained.
There is an apparent paradox in considering static friction as maintaining
the condition for rolling without slipping. Consider a round object of mass M
and radius R rolling along a horizontal, level surface.

The free-body diagram would have three forces acting on the object: the frictional force fs, the weight, and the normal force of the surface on the object. Clearly the weight and normal force cancel so that the net force in the vertical direction is zero. However, the object rolls with no loss in the horizontal velocity if it is perfectly rigid. How can this be? Think back to things as operating through the work-energy theorem. The work done by forces must change the kinetic energy. However, in this case, since the point of contact is instantaneously at rest, the friction force does not operate over any distance and hence does not change the translational velocity. If we switch from rolling on a level surface to rolling on an incline, however, the situation changes dramatically.

Solution: We can start by drawing the free-body diagram as shown in
the figure above. Since there is rolling without slipping, static friction is
acting and we therefore will not need to know what FN is since the
static friction can be any magnitude between 0 and musFN. The forces acting in the x
direction yield:
| Mgsin(theta) - fs | = MaCM |
The frictional force causes a torque about an axis going through the
geometric center of the sphere.
where the minus sign results from the fact that the torque tends to make
the sphere want to rotate in the clockwise direction and the convention in the
text is that torques that make clockwise rotations are negative. If rolling
without slipping is occuring, then alpha = -aCM/R (again the minus
sign results since positive aCM corresponds to clockwise rotation).
Since I for a sphere is 2/5 MR2, we have
| -fsR | = -(2/5)MR2aCM/R ==> |
| fs | = (2/5)MaCM |
Plugging this back into our force equation, we get
| Mgsin(theta) - fs | = MaCM |
| Mgsin(theta) - (2/5)MaCM | = MaCM ==> |
| aCM | = (5/7)g sin(theta) |
Now we have a paradox? If in rolling motion the force of friction does no
work, why do we have an acceleration here which is less than g sin(theta)? This
will lead to a translational velocity that is less than the sqrt[2gh] that we
expect if only gravity is doing work on the sphere. The answer, of course, is
that some of the work done by gravity leads to increasing the translational
velocity and some goes to increasing the rotational velocity. Hence, we can
conjecture that the total kinetic energy of an object must be given by the sum
of its rotational kinetic energy, ½ I*omega2 and its translational
kinetic energy ½ mv2. To see that this works out for the case at
hand, let's use the acceleration we derived to work out what the translational
and rotational velocities are at the end of the ramp. Note that d is the total
distance traveled along the ramp in the following equations.
| v2 | = v02 + 2aCMd |
| = 2(5/7)g*sin(theta)*d | |
| omega2 | = omega02 + 2*alpha*phi |
| = 2*alpha*phi |
For the last term, phi is the total angular displacement of the sphere as it
rolls down the ramp. Since the translation of the center-of-mass is the same as
the arc-length traveled for rolling without slipping, phi = d/R and alpha =
aCM/R, so omega2 = 2aCMd/R2. This is
precisely v2/R2 as we expect for rolling without slipping.
Furthermore, if we note that the height, h, is equal to d*sin(theta), then the
total kinetic energy can be expressed as
| Ktrans. + Krot. | = ½ Mv2 + ½ I*omega2 |
| = ½ M[2(5/7)g*sin(theta)*d] + ½ (2/5 MR2)* [2(5/7)*g*sin(theta)*d/R2] | |
| = M[(5/7)g*h] + 1/5 M[2(5/7)*g*h] | |
| = (5/7)Mgh + (2/7)Mgh | |
| Ktrans. + Krot. | = Mgh |
So the total work done by gravity, Mgh, is just equal to the change in the total kinetic energy, provided we express the total kinetic energy as Ktrans. + Krot..



Next: Rolling Motion cont'd. Up: Completing the Circle Previous: Moments of Inertia
larryg@upenn5.hep.upenn.edu